[ML] Convolution 정리

Convolution이 무엇인가요?

예전 기술면접때 convolution이 무엇인지에 대한 질문을 받은 적 있다. tensorflow, pytorch에 구현된 convolution 연산을 사용해 비전이나 NLP에 사용되는 신경망을 학습했지만, 무엇인지에 대해 물었을 때 말로 풀어서 대답하기 어려웠다. 분명 머릿속엔 그림이나 연산 과정을 떠올릴 수 있지만 어떤 의미를 가지는지, 연산 결과값이 어떻게 사용되는지 몰랐던 것 같다. 그래서 이번에 convolution에 대해 정리하고 연산이 어떠한 의미를 가지는지 정리하고자 한다.

딥러닝을 하면서 convolution layer 용어를 많이 사용하기 때문에 convolution은 신경망에서 비롯된것인 줄 알았으나 실제로는 두 개의 함수가 t 시점에서 얼마나 overlap이 되었는지 계산하는 연산이었다(t에 대한 함수).

그리고 일반적으로 범위를 infinite로 해서 표기한다.

두 함수에 대한 convolution 연산은 아래 그림과 같다.

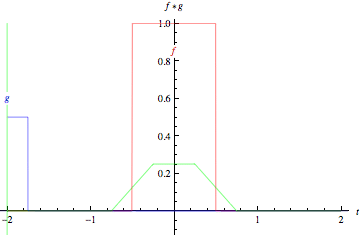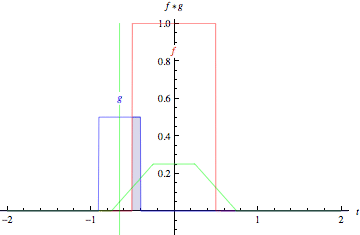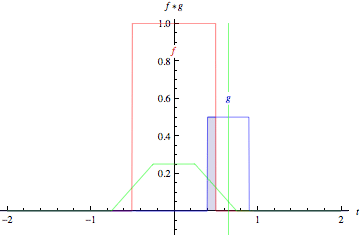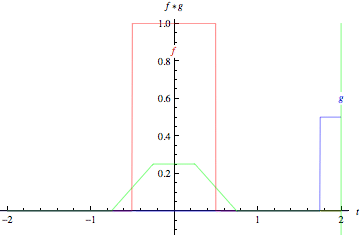
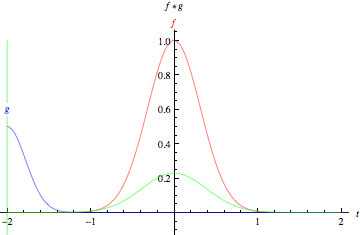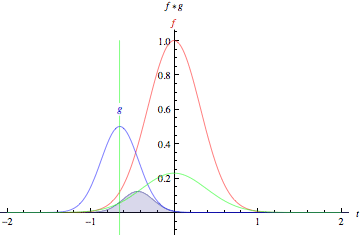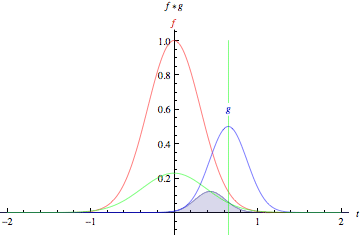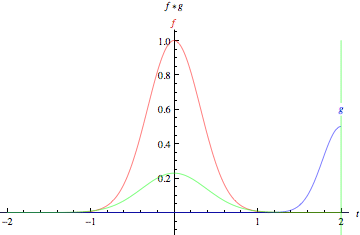
첫 번째 그림은 두 개의 boxcar function(박스 모양의 함수), 아래는 두 개의 Gaussian에 대한 convolution 연산이다. 각각의 그림에서 녹색 실선은 함수 f(빨간색), 함수 g(파란색)의 convolution 연산 결과를 의미한다. 함수 g에서 녹색 수직선은 t 시점을 의미한다. t가 변하면서 생기는 회색 영역은 $g(\tau)f(t-\tau)$값을 의미한다. 그림에서 보이듯 두 함수의 겹치는 영역이 커지면 convolution 결과 값이 커지게됨을 알 수 있다.

신경망에서 사용되는 convolution 연산도 이와 비슷하다고 볼 수 있다.

위의 그림을 보면, 입력 이미지로부터 Feature Detector(filter, kernel이라고도 불림; CNN의 학습 파라미터)로 convolution 연산을 수행해 결과로 feature map을 만들게 된다. 따라서 feature map은 feature detector의 패턴이 입력 이미지에 얼마나 잘 나타나있는지에 대한 정보를 가지게 된다. 게다가 논문에서는 convolution 연산은 spatial invariance라는 표현을 사용하는걸 자주 볼 수 있는데, filter의 패턴이 입력 이미지 어디에 있던지간 convolution 연산을 하면 feature map에 패턴 정보가 담기게 된다는 의미이다.

CNN(Convolution Neural Networks)의 구조 대부분은 convolution layer파트와 fully connected layer 파트 두 가지로 구성되어 있다. 입력 이미지로부터 filter와 convolution을 통해 filter의 패턴이 입력 이미지에 얼마나 나타나있는지에 대한 정보를 파악한 뒤, 이러한 feature를 바탕으로 fully connected layer에서 비선형 관계를 학습하는 구조가 되겠다.

[Reference]

• https://mathworld.wolfram.com/Convolution.html
• https://www.slideshare.net/KirillEremenko/deep-learning-az-convolutional-neural-networks-cnn-step-1-convolution-operation